FÍSICA-- TEOREMA DE STEVIN,TEOREMA DE PASCAL,EMPUXO,FORÇA GRAVITACIONAL, LEIS DE KEPLER E UNIDADES ASTRONÔMICAS.
Teorema de Stevin
Seja um líquido qualquer de densidade d em um recipiente qualquer.
Escolhemos dois pontos arbitrários R e T.
As pressões em Q e R são:
A diferença entre as pressões dos dois pontos é:
|
Teorema de Stevin: "A diferença entre as pressões de dois pontos de um fluido em equilíbrio é igual ao produto entre a densidade do fluido, a aceleração da gravidade e a diferença entre as profundidades dos pontos." |
Através deste teorema podemos concluir que todos os pontos a uma mesma profundidade, em um fluido homogêneo (que tem sempre a mesma densidade) estão submetidos à mesma pressão.
Teorema de Pascal
Quando aplicamos uma força a um líquido, a pressão causada se distribui integralmente e igualmente em todas as direções e sentidos.
Pelo teorema de Stevin sabemos que:
Então, considerando dois pontos, A e B:
Ao aplicarmos uma força qualquer, as pressões no ponto A e B sofrerão um acréscimo:
Se o líquido em questão for ideal, ele não sofrerá compressão, então a distância h, será a mesma após a aplicação da força.
Assim:
Teorema de Pascal:
"O acréscimo de pressão exercida num ponto em um líquido ideal em equilíbrio se transmite integralmente a todos os pontos desse líquido e às paredes do recipiente que o contém."
Prensa hidráulica
Uma das principais aplicações do teorema de Pascal é a prensa hidráulica.
Esta máquina consiste em dois cilindros de raios diferentes A e B, interligados por um tubo, no seu interior existe um líquido que sustenta dois êmbolos de áreas diferentes e
.
Se aplicarmos uma força de intensidade F no êmbolo de área , exerceremos um acréscimo de pressão sobre o líquido dado por:
Pelo teorema de Pascal, sabemos que este acréscimo de pressão será transmitido integralmente a todos os pontos do líquido, inclusive ao êmbolo de área , porém transmitindo um força diferente da aplicada:
Como o acréscimo de pressão é igual para ambas as expressões podemos igualá-las:
Exemplo:
Considere o sistema a seguir:
Dados:
Qual a força transmitida ao êmbolo maior?
Empuxo
Ao entrarmos em uma piscina, nos sentimos mais leves do que quando estamos fora dela.
Isto acontece devido a uma força vertical para cima exercida pela água a qual chamamos Empuxo, e a representamos por .
O Empuxo representa a força resultante exercida pelo fluido sobre um corpo. Como tem sentido oposto à força Peso, causa o efeito de leveza no caso da piscina.
A unidade de medida do Empuxo no SI é o Newton (N).
Princípio de Arquimedes
Foi o filósofo, matemático, físico, engenheiro, inventor e astrônomo grego Arquimedes (287a.C. - 212a.C.) quem descobriu como calcular o empuxo.
Arquimedes descobriu que todo o corpo imerso em um fluido em equilíbrio, dentro de um campo gravitacional, fica sob a ação de uma força vertical, com sentido oposto à este campo, aplicada pelo fluido, cuja intensidade é igual a intensidade do Peso do fluido que é ocupado pelo corpo.
Assim:
onde:
=Empuxo (N)
=Densidade do fluido (kg/m³)
=Volume do fluido deslocado (m³)
g=Aceleração da gravidade (m/s²)
Exemplo:
Em um recipiente há um líquido de densidade 2,56g/cm³. Dentro do líquido encontra-se um corpo de volume 1000cm³, que está totalmente imerso. Qual o empuxo sofrido por este corpo? Dado g=10m/s²
|
Saiba mais... Se:
|
Peso aparente
Conhecendo o princípio de Arquimedes podemos estabelecer o conceito de peso aparente, que é o responsável, no exemplo dado da piscina, por nos sentirmos mais leves ao submergir.
Peso aparente é o peso efetivo, ou seja,aquele que realmente sentimos. No caso de um fluido:
Força gravitacional
Ao estudar o movimento da Lua, Newton concluiu que a força que faz com que ela esteja constantemente em órbita é do mesmo tipo que a força que a Terra exerce sobre um corpo em suas proximidades. A partir daí criou a Lei da Gravitação Universal.
Lei da Gravitação Universal de Newton:
"Dois corpos atraem-se com força proporcional às suas massas e inversamente proporcional ao quadrado da distância que separa seus centros de gravidade."
Onde:
F=Força de atração gravitacional entre os dois corpos
G=Constante de gravitação universal
M e m = massa dos corpos
d=distância entre os centros de gravidade dos corpos.
Nas proximidades da Terra a aceleração da gravidade varia, mas em toda a Litosfera (camada em que há vida) esta pode ser considerada constante, seus valores para algumas altitudes determinadas são:
| Altitude (km) | Aceleração da Gravidade (m/s²) | Exemplo de altitude |
|---|---|---|
|
0
|
9,83
|
nível do mar
|
|
8,8
|
9,80
|
cume do Monte Everest
|
|
36,6
|
9,71
|
maior altura atingida por balão tripulado
|
|
400
|
8,70
|
órbita de um ônibus espacial
|
|
35700
|
0,225
|
satélite de comunicação
|
Leis de Kepler
Quando o ser humano iniciou a agricultura, ele necessitou de uma referência para identificar as épocas de plantio e colheita.
Ao observar o céu, os nossos ancestrais perceberam que alguns astros descrevem um movimento regular, o que propiciou a eles obter uma noção de tempo e de épocas do ano.
Primeiramente, foi concluído que o Sol e os demais planetas observados giravam em torno da Terra. Mas este modelo, chamado de Modelo Geocêntrico, apresentava diversas falhas, que incentivaram o estudo deste sistema por milhares de anos.
Por volta do século XVI, Nicolau Copérnico (1473-1543) apresentou um modelo Heliocêntrico, em que o Sol estava no centro do universo, e os planetas descreviam órbitas circulares ao seu redor.
No século XVII, Johanes Kepler (1571-1630) enunciou as leis que regem o movimento planetário, utilizando anotações do astrônomo Tycho Brahe (1546-1601).
Kepler formulou três leis que ficaram conhecidas como Leis de Kepler.
1ª Lei de Kepler - Lei das Órbitas
Os planetas descrevem órbitas elipticas em torno do Sol, que ocupa um dos focos da elipse.
2ª Lei de Kepler - Lei das Áreas
O segmento que une o sol a um planeta descreve áreas iguais em intervalos de tempo iguais.
3ª Lei de Kepler - Lei dos Períodos
O quociente dos quadrados dos períodos e o cubo de suas distâncias médias do sol é igual a uma constante k, igual a todos os planetas.
Como o período de rotação de um planeta é equivalente a um ano, conclui-se que quanto mais longe o planeta estiver do Sol, mais longo será seu período de rotação, e em consequência "seu ano".
Unidades Astronômicas
No estudo de astronomia muitas vezes as unidades do Sistema Internacional (SI) são ineficientes pois as distâncias que devem ser expressas são muito grandes.
Por exemplo: A distância da Terra até Marte é de cerca de 75 milhões de quilômetros, que no SI é expresso por 75 000 000 000 metros.
Devido à necessidade de unidades mais eficientes são utilizadas: Unidade Astronômica (UA), Anos-luz (AL) e Parsec (Pc).
Unidade Astronômica (UA)
É a distância média entre a Terra e o Sol. É empregada principalmente para descrever órbitas e distâncias dentro do Sistema Solar.
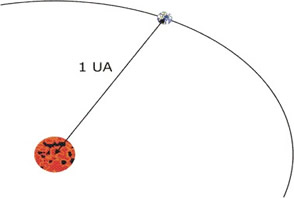
![]()
O tamanho médio da órbita dos planetas do Sistema Solar, ou seja, sua distância ao Sol é:
|
Planeta
|
Distância ao Sol (UA)
|
|
Mercúrio
|
0,39
|
|
Vênus
|
0,72
|
|
Terra
|
1,00
|
|
Marte
|
1,52
|
|
Júpter
|
5,20
|
|
Saturno
|
9,53
|
|
Urano
|
19,10
|
|
Netuno
|
30,00
|
Ano-Luz (al)
É a distância percorrida pela luz, no vácuo, no tempo de 1 ano terrestre.
Sendo a velocidade da luz c = 299 792,458 km/s, temos que:
1 al = 9 460 536 207 068 016 m = 63241,07710 UA
A estrela mais próxima do Sol é chamada Próxima Centauri, localizada na constelação de Centauro. A sua distância ao Sol é de 4,22 al
Parsec (Pc)
É a distância na qual 1 UA é representada por 1'' (1 segundo de arco), em uma medição por paralaxe.
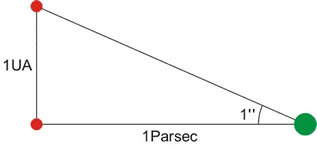
Esta unidade é usada para distância muito grandes, como a distância entre estrelas, entre galáxias ou de objetos muito distantes, como quasares.
![]()

